Словарь
Скачать краткий словарь терминов
Материал взят с сайта Учитель.Про
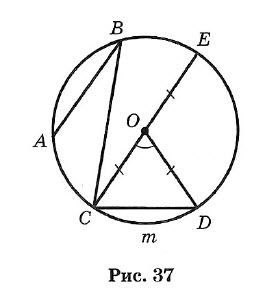Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).
Материал взят с сайта Учитель.Про
«Краткий курс геометрии 8 класс»
«Краткий курс геометрии 8 класс» — это краткие теоретические сведения по курсу геометрии за 8 класс (определения, теоремы, основные свойства). Цитаты взяты в учебных целях из пособия «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ (базовый уровень): 8 класс / Э.Н.Бабаян. — Ростов н/Д: Феникс.
Планиметрия
1. Многоугольник
ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).
Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).
Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.
2. Правильные многоугольники
Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.
Свойства
1. Каждый угол правильного n-угольника равен аn = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).
Свойства
1. Каждый угол правильного n-угольника равен аn = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).
3. Четырехугольник
4. Параллелограмм
Признаки параллелограмма (рис. 48)
- Если в четырехугольнике две стороны равны и параллельны (АВ = DC, АВ || CD), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике противоположные стороны попарно равны (АВ = DC, AD = DC), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике противоположные углы попарно равны (∠A = ∠C; ∠B = ∠D), то такой четырехугольник — параллелограмм.
- Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то такой четырехугольник — параллелограмм.
5. Трапеция
Равнобедренная трапеция
Прямоугольная трапеция
6. Прямоугольник
7. Ромб
8. Квадрат
9. Теорема Чевы
10. Теорема Менедая
11. Теорема синусов
12. Теорема косинусов
13. Площадь треугольника
14. Площадь многоугольников
15. Равносторонний (правильный) треугольник
16. Подобные треугольники
17. Признаки подобия треугольников
18. Окружность
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).
19. Свойства касательных к окружности
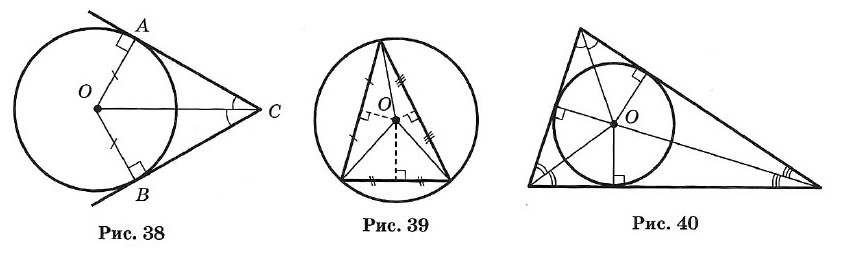
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
20. Окружность и треугольник
1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).
21. Окружность и четырехугольник
22. Углы и окружность
23. Метрические соотношения в окружности
24. Длина окружности. Площадь круга и его частей
25. Уравнение окружности
Комментарии
Отправить комментарий